«ΤΑ ΝΕΑ» σε συνεργασία με τον φροντιστηριακό όμιλο «Ομόκεντρο» και τους καθηγητές τους παρουσιάζουν τα SOS των πανελλαδικών εξετάσεων ανά μάθημα. Σήμερα τα θέματα της Ανάπτυξης Εφαρμογών σε Προγραμματιστικό Περιβάλλον και των Μαθηματικών Προσανατολισμού.
Μαθηματικά Προσανατολισμού
Θεωρήματα με ονοματεπώνυμο:
1) Θ. Bolzano
Εφαρμόζεται σε ασκήσεις όπου ζητείται να αποδείξουμε ότι μια εξίσωση f(x)=0 (ή f(x)=g(x)) έχει μία τουλάχιστον ρίζα στο (α, β).
ΠΡΟΣΟΧΗ στη διατύπωση και στη γεωμετρική ερμηνεία.
2) Θεώρημα Ενδιάμεσων Τιμών (ΘΕΤ)
Εφαρμόζεται όταν θέλουμε να αποδείξουμε ότι μια συνάρτηση f παίρνει μια τιμή σε ένα ανοιχτό διάστημα (α, β).
ΠΡΟΣΟΧΗ στη διατύπωση, στην απόδειξη και στη γεωμετρική ερμηνεία.
3) Θεώρημα Μεγίστου Ελαχίστου
Αν μια συνάρτηση είναι συνεχής στο [α, β] τότε παίρνει πάντα μια ελάχιστη τιμή m και μια μέγιστη τιμή Μ στο διάστημα αυτό και ισχύει πάντα m≤f(x)≤M για κάθε xЄ[α, β].
4) Θεώρημα Παράγωγος και Συνέχεια
• Αν μια συνάρτηση είναι παραγωγίσιμη σε ένα σημείο x0 του πεδίου ορισμού της τότε είναι και συνεχής στο x0.
• ΠΡΟΣΟΧΗ ΣΤΗΝ ΑΠΟΔΕΙΞΗ
Το αντίστροφο δεν ισχύει. Δηλαδή αν η f είναι συνεχής στο x0 δεν είναι κατ’ ανάγκη και παραγωγίσιμη στο x0.
• Αν όμως η f δεν είναι συνεχής στο x0 τότε δεν είναι και παραγωγίσιμη στο x0.
5) Θεώρημα Rolle
ΠΡΟΣΟΧΗ στη διατύπωση και στη γεωμετρική ερμηνεία. Εφαρμόζεται στην f στο [α, β] και αποδεικνύει ότι η f΄ έχει μία τουλάχιστον ρίζα στο (α, β).
6) Θεώρημα Μέσης Τιμής (ΘΜΤ)
ΠΡΟΣΟΧΗ στη διατύπωση και στη γεωμετρική ερμηνεία. Εφαρμόζεται για την f 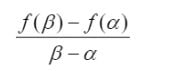
στο [α, β] και αποδεικνύει ότι η f΄ παίρνει την τιμή
7) Θεώρημα Fermat
Διατύπωση: Εστω μια συνάρτηση f ορισμένη σε ένα διάστημα Δ και x0 ένα εσωτερικό σημείο του Δ. Αν η f παρουσιάζει τοπικό ακρότατο στο x0 και είναι παραγωγίσιμη στο x0 τότε f΄(x0)=0.
Απόδειξη: Σχολικό βιβλίο σελίδα 142 (ΠΟΛΥ ΠΡΟΣΟΧΗ ΣΤΗΝ ΑΠΟΔΕΙΞΗ)
ΠΡΟΣΟΧΗ: Το αντίστροφο του θεωρήματος δεν ισχύει.
Σπουδαίες επισημάνσεις:
1. Πρέπει να γνωρίζουμε να συνθέτουμε δύο συναρτήσεις, αλλά να μπορούμε και να τις «αποσυνθέτουμε».
2. Στην εύρεση αντίστροφης συνάρτησης δεν ξεχνάμε τους περιορισμούς του ψ, όταν διαιρούμε, λογαριθμούμε, υψώνουμε σε άρτια δύναμη, βάζουμε ρίζες.
3. Σε ένα όριο εντoπίζουμε πρώτα το είδος της απροσδιοριστίας.
4. Πρέπει να μπορούμε να βρίσκουμε την εφαπτομένη της γραφικής παράστασης μιας συνάρτησης σε ένα σημείο του πεδίου ορισμού της.
5. Για μονοτονία και ακρότατα μελετάμε το πρόσημο της πρώτης παραγώγου.
6. Το ολικό ακρότατο είναι και τοπικό. Ενα τοπικό ελάχιστο μπορεί να είναι μεγαλύτερο από ένα τοπικό μέγιστο.
7. Οταν μας δίνουν δεδομένη ανίσωση το πρώτο που σκεφτόμαστε είναι το θεώρημα Fermat. Σε ανίσωση που δεν περιέχει ισότητα δεν εφαρμόζουμε θεώρημα Fermat. Τη χρησιμοποιούμε για να βρούμε πρόσημο.
8. Για την κυρτότητα και τα σημεία καμπής μελετάμε το πρόσημο και τις ρίζες της δεύτερης παραγώγου.
ΠΡΟΣΟΧΗ: Η πρόταση: Αν f΄΄(x0)=0 τότε η f παρουσιάζει καμπή στο σημείο Μ(x0, f(x0)) είναι λανθασμένη διότι π.χ. η f(x)=x4 έχει f΄΄(0)=0 όμως η f δεν παρουσιάζει καμπή στο Ο(0, f(0)).
9. Για να βρούμε τις ασύμπτωτες της γραφικής παράστασης θα εξετάσουμε το πεδίο ορισμού της.
10. Πρέπει να μπορούμε να μελετάμε μια συνάρτηση και με τη χρήση του πίνακα μεταβολών της να σχεδιάζουμε τη γραφική παράστασή της.
11. Πρέπει να μπορούμε να βρίσκουμε τις Αρχικές των βασικών συναρτήσεων.
12. Οταν ζητάμε εμβαδό χωρίου πρέπει να ελέγχουμε τη συνέχεια της f και το πρόσημό της.
ΠΡΟΣΟΧΗ: Διαβάζουμε πολύ καλά τα σχόλια και τις παρατηρήσεις του σχολικού βιβλίου για να απαντήσουμε σωστά στις ερωτήσεις ΣΩΣΤΟΥ-ΛΑΘΟΥΣ.
Ο Παναγιώτης Κούσης είναι μαθηματικός στα φροντιστήρια «Ομόκεντρο»
Ανάπτυξη εφαρμογών σε προγραμματιστικό περιβάλλον
1. Ανάλυση Προβλήματος
Οι ορισμοί του κεφαλαίου.
2. Βασικές Εννοιες Αλγορίθμων
Ορισμός αλγορίθμου.
Μετατροπή ενός διαγράμματος ροής σε ψευδογλώσσα και το αντίστροφο.
Να ξεχωρίζω την απλή επιλογή Αν από τη σύνθετη και την πολλαπλή.
Να χρησιμοποιώ την εντολή Επίλεξε.
Μετατροπή της εντολής επανάληψης ΓΙΑ σε ΟΣΟ και ΜΕΧΡΙΣ_ΟΤΟΥ και αντίστροφα.
3. Δομές Δεδομένων και Αλγόριθμοι
Να ξεχωρίζω τις στατικές και τις δυναμικές δομές.
Να γνωρίζω καλά τη δομή της στοίβας και της ουράς και να μπορώ να λύνω με τη βοήθεια μονοδιάστατου πίνακα ασκήσεις στοίβας και ουράς.
Να γνωρίζω καλά τα πλεονεκτήματα και τα μειονεκτήματα μιας λίστας και ενός πίνακα.
Να μάθω τις ασκήσεις που σχετίζονται με τα δέντρα.
Να μάθω πάρα πολύ καλά τη σειριακή και τη δυαδική αναζήτηση καθώς επίσης και τη μέθοδο της ευθείας ανταλλαγής (bubble).
4. Τεχνικές Σχεδίασης Αλγορίθμων
Να κατανοήσω τη μέθοδο Διαίρει και Βασίλευε καθώς και πού μπορεί να εφαρμοστεί.
6. Εισαγωγή στον Προγραμματισμό
Να κατανοήσω και να ξεχωρίζω τις βασικές τεχνικές σχεδίασης προγραμμάτων.
Να μάθω τα πλεονεκτήματα, τα μειονεκτήματα και τις ομοιότητες μεταξύ διερμηνευτή και μεταγλωττιστή.
Να μετατρέπω ένα πρόγραμμα που περιέχει την εντολή Go to σύμφωνα με τις αρχές του δομημένου προγραμματισμού.
7 και 8. Βασικές Εννοιες Προγραμματισμού – Επιλογή και Επανάληψη
Να μάθω τη μεθοδολογία επίλυσης των ασκήσεων όταν το πλήθος των επαναλήψεων καθορίζεται από την εκφώνηση, το δίνει ο χρήστης ή είναι άγνωστο.
Να μελετήσω τις ασκήσεις μεγίστου – ελαχίστου, κλιμακωτής χρέωσης και ελέγχου εισαγωγής δεδομένων.
9. Πίνακες
Να μελετήσω τις ασκήσεις του κεφαλαίου τόσο για τους μονοδιάστατους όσο και για τους πίνακες δύο διαστάσεων.
Να μπορώ να βρω το άθροισμα, το πλήθος, το μεγαλύτερο και το μικρότερο στοιχείο, να αναζητώ ένα στοιχείο και να ελέγχω αν πληροί μια ιδιότητα ένας πίνακας.
Οταν έχουμε έναν δισδιάστατο πίνακα, να βρίσκω άθροισμα, πλήθος, μέγιστο και ελάχιστο στοιχείο και ταξινόμηση μιας (κάθε) γραμμής ή στήλης.
10. Υποπρογράμματα
Ορισμός διαδικασίας και συνάρτησης.
Μετατροπή συνάρτησης σε διαδικασία και αντίστροφα όταν μπορεί να γίνει.
Να ξεχωρίζω τις πραγματικές και τις τυπικές παραμέτρους καθώς και τους κανόνες που τις διέπουν.
11. Σύγχρονα Προγραμματιστικά Περιβάλλοντα
Ορισμός του αντικειμενοστραφούς προγραμματισμού (αντικείμενα, χαρακτηριστικά και μέθοδοι).
Ομαδοποίηση των αντικειμένων σε κλάσεις και διαγραμματική αναπαράσταση αυτών.
Δημιουργία υπερκλάσεων.
Κατανόηση της έννοιας του πολυμορφισμού.
13. Εκσφαλμάτωση Προγράμματος
Να αναγνωρίζω τα συντακτικά λάθη, τα λάθη που οδηγούν σε αντικανονικό τερματισμό του προγράμματος και τα λογικά λάθη ενός προγράμματος.
Να κατανοήσω τη μέθοδο ελέγχου Μαύρο Κουτί.
Ο Αντώνης Παβίτσος είναι καθηγητής Πληροφορικής στα φροντιστήρια Ομόκεντρο
in.gr









































.jpg)






















Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου